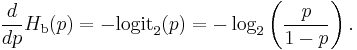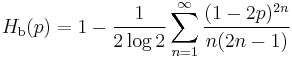Binary entropy function

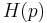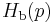In information theory, the binary entropy function, denoted H(p) \, or H_{\mathrm b}(p) \,, is defined as the entropy of a Bernoulli trial with probability of success p. Mathematically, the Bernoulli trial is modelled as a random variable X that can take on only two values: 0 and 1. The event 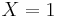X = 1 is considered a success and the event 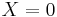X = 0 is considered a failure. (These two events are mutually exclusive and exhaustive.)

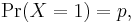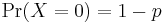If \mathrm{Pr}(X=1) = p, then \mathrm{Pr}(X=0) = 1-p and the entropy of X is given by

H(X) = H_{\mathrm b}(p) = -p \log_2 p - (1 - p) \log_2 (1 - p). \,

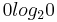where 0 log_2 0 is taken to be 0. The logarithms in this formula are usually taken (as shown in the graph) to the base 2. See binary logarithm.

When 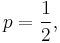p=\frac 1 2 , the binary entropy function attains its maximum value. This is the case of the unbiased bit, the most common unit of information entropy.

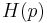H(p) is distinguished from the entropy function by its taking a single scalar constant parameter. For tutorial purposes, in which the reader may not distinguish the appropriate function by its argument, 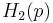H_2(p) is often used; however, this could confuse this function with the analogous function related to Rényi entropy, so 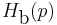H_\mbox{b}(p) (with "b" not in italics) should be used to dispel ambiguity.

Contents

Derivative

The derivative of the binary entropy function may be expressed as the negative of the logit function:

{d \over dp} H_{\mathrm b}(p) = - \operatorname{logit}_2(p) = -\log_2\left( \frac{p}{1-p} \right). \,

Taylor series

The Taylor series of the binary entropy function in a neighbourhood of 1/2 is

H_{\mathrm b}(p) = 1 - \frac{1}{2\log2} \sum^{\infin}_{n=1} \frac{(1-2p)^{2n}}{n(2n-1)}

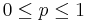
for 0\le p\le 1

See also

References